Assignment 9: Many processes make light work

Due Wednesday, March 22, at midnight

The goals for this assignment are:

Brush off your C programming
Implement an algorithm using multiple processes with fork()

Update your repository

Do a fetch upstream to obtain the basecode for this assignment.

Using the command line

Open terminal and change your current directory to your assignment repository.
Run the command git fetch upstream
Run the command git merge upstream/master

Your repository should now contain a new folder named A08.

The fetch and merge commands update your repository with any changes from the original.

1. Warm-up

In the file, warmup.c, implement a program that spawns processes according to the following diagram.

$ make warmup
gcc -g -Wall -Wvla -Werror warmup.c -o warmup
$ ./warmup
17300] A0
17300] B0
17301] B1
17301] Bye
17300] C0
17300] Bye
17302] C1
17302] Bye

Requirements:

Your program should print the messages as shown above.
Your program should use fork() to spawn processes.
Call getpid() to show the process ids for each print message.

2. Mandelbrot

In the file, single_mandelbrot.c, compute a program that outputs a PPM image of the mandelbrot set. You have been given basecode that initializes the following values from command line arguments. This code uses the getopt function.

Arguments:

-s <size> the image width and height
-l <xmin> the leftmost coordinate, e.g. minimum x value
-r <xmax> the rightmost coordinate, e.g. maximum x value
-t <ymin> the topmost coordinate, e.g. minimum y value
-b <ymax> the bottommost coordinate, e.g. maximum y value

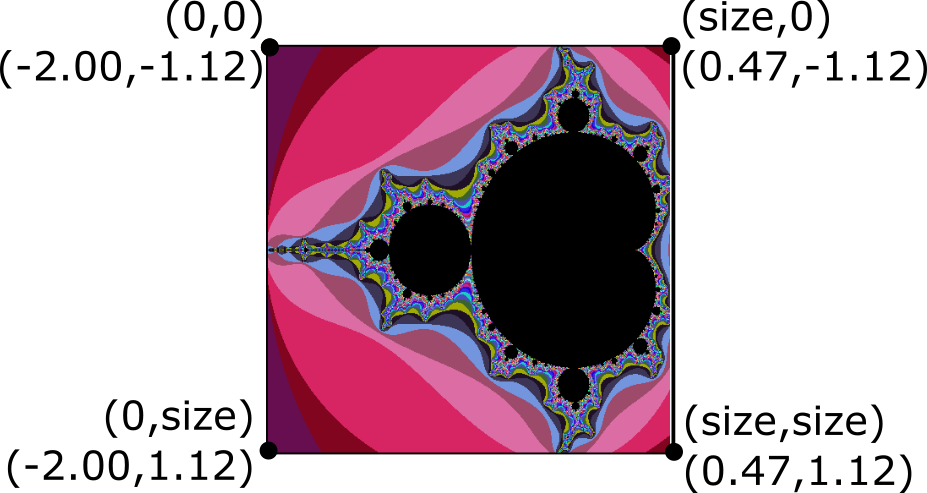
When you run your program, you should get the output such as the following

$ make single_mandelbrot
$ ./single_mandelbrot
Generating mandelbrot with size 480x480
  X range = [-2.0000,0.4700]
  Y range = [-1.1200,1.1200]
Computed mandelbrot set (480x480) in 0.323261 seconds
Writing file: mandelbrot-480-1649001071.ppm

Requirements and hints:

You should re-use your PPM functions from A06.
Allocate an array of pixels using malloc and then save the final image using write_ppm.
You should output the number of seconds needed to compute the image. Use this class example, matrix.c for an example.
Your output filename should have the format mandelbrot-<size>-<timestamp>.ppm. The timestamp can be obtained by calling time(0).
Set a random seed to ensure that the color palette is different each time, e.g. srand(time(0))
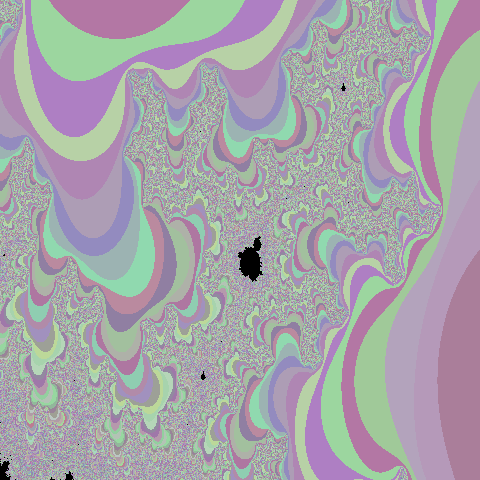
(Optional) Experiment with visualizing other regions of the mandelbrot set. For example, if you run with ./single_mandelbrot -s 480 -l -0.02524993 -r 0.00975 -b -0.8172 -t -0.79725, you get the following image

2.1. Background: Mandelbrot Set

The mandelbrot set is fractal popularized by Benoit Mandelbrot in 1980.

The mandelbrot set consists of the set of complex numbers z for which \(z^2 + c\) does not diverge to infinity when z starts at 0. To visualize this set, recall that a complex number, \(z = x + yi\), can be visualized as a 2D point \((x,y)\). Although the set derives from complex numbers, we can compute the set by thinking about 2D coordinates, \((x,y)\).

To see whether the complex number \((x,y)\) diverges, we simply need a loop that repeatedly computes \(z^2 + c\). If we expand the complex number multiplication of \(z = x + y*i\), z will change each iteration based on the following algorith. To test for divergence, we check whether z goes out of the bounds of 4*4. If z does go out of bounds, we assign it a color based on how quickly it "escaped" the distance 4*4. If after MAX iterations, z is still smaller than 4*4, it belongs to the set and we color it black.

The last thing we need to draw the set is the region of values for x and y that bound the set. X should vary from -2.0 to 0.47. Y should vary from -1.12 to 1.12. Here is the full algorithm. Assume that the image width and height are the same, e.g. square images.

for each row in the image
   for each col in the image
      xfrac = row / image_size
      yfrac = col / image_size
      x0 = xmin + xfrac * (xmax - xmin)
      y0 = ymin + yfrac * (ymax - ymin)

      x = 0
      y = 0
      iter = 0
      while (iter < MAX && x*x + y*y < 2*2)
        xtmp = x*x - y*y + x0
        y = 2*x*y + y0
        x = xtmp
        iter++

      if (iter < MAX) // escaped
        color = palette[iter]
      else
        color = black

      write color to image at location (row,col)

Palette

The palette should contain the same number of colors as MAX iterations. Use ppm_pixel to represent colors in the pallet. You can either generate random colors or compute a base color and jitter it e.g.

for each palette color
  red = rand() % 255
  green = rand() % 255
  blue = rand() % 255

basered = rand() % 255
basegreen = rand() % 255
baseblue = rand() % 255
for each palette color
  red = basered + rand() % 100 - 50
  green = basegreen + rand() % 100 - 50
  blue = baseblue + rand() % 100 - 50

3. Submit your work

Submit your code and images

1) Push your code work to github

$ git status
$ git add .
$ git status
$ git commit -m "assignment complete"
$ git status
$ git push
$ git status